Quantum error correction is correcting better to record low rates

(By Amara Graps) If my favorite, songwriter-musician, the late Jerry Garcia were alive today, he might appreciate: the fundamental role of quantum error correction (QEC) in quantum computing, QEC’s interdisciplinary quality between Information Theory, Computer Science, Applied Mathematics, Physical Science, and QEC’s strange-ish links to black holes,

Because, on a riff of his own in the song: Truckin’:

What a looooooooong strange trip it’s been!

are road-worthy quips by august members in the Quantum Computing field:

• Quantum computers are held back by a single bottleneck – their susceptibility to error. —Michael Biercuk, 21 December, 2021 IQT
• We may have a long road ahead to practical applications, and Quantum Error Correction is most likely the key to getting there. —John Preskill, 8 December 2021, Q2B Conference
• But researchers are only now starting to make such error correction work in the real world, and actually putting it to use will take much longer. —Scott Aaronson, 8 June, 2021 Quanta Magazine

Protecting Quantum Encoded Information from Noise

The reason that quantum error correction is such a challenging journey is the same reason why coherent quantum systems are so fragile: the noise characteristics of the experimental devices. To reach the goal of universal quantum computation, we must have methods of achieving a scalable, fault-tolerant, i.e., fully, error-correcting, logical qubit. Figure 1 illustrates the essential steps:

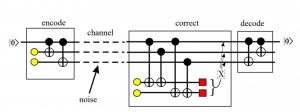
Figure 1. A three-qubit code circuit diagram of the encoding, correcting, & decoding from Marshall Pickett’s thesis.

Quantum information processing is fundamentally different from classical, which has robust, discrete on/off states. First in the quantum information coherence, i.e. superpositions of non-discrete states, that must be preserved, and second, in the type of noise processes, which can change the amplitudes and phases of the superposed quantum states. These differences followed the 1982 quantum no-cloning theorem constraint, which prohibits states of the qubits to be copied.

To preserve the state of superposition of the encoded qubit, one measures the errors (‘decoherence’) that occur, using stabilizer codes (see the ‘correct box’ in Fig. 1). These codes measure ancillary qubits (yellow filled circles in Fig. 1) without measuring the state of the data qubits, which would collapse the state of the system.

In 2021, QEC made solid achievements.

Real-Time QEC

A full demonstration of the necessary components for a fault-tolerant  implementation of a QEC code, capable of repeatedly correcting all single-qubit errors was achieved in  Ryan-Anderson et al, 2021’s work “Realization of Real-Time Fault-Tolerant Quantum Error Correction”, published December 23, 2021. Their work initialized a logical Pauli basis (a projection of the electron spin onto the  x,y,z axes) using an encoded circuit, based on ten ¹⁷¹Yb⁺ qubit trapped ions, ran multiple adaptive QEC cycles, measured physical qubits while tracking corrections, ran a decoding algorithm, and updated the corrections after each QEC cycle. Real-time.

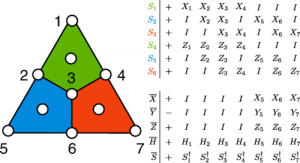
Figure 2. QEC code. Physical qubits are indicated by white circles. The seven data qubits are on the vertices of the polygons, and three ancilla qubits for the measurements are in the center of each polygon.  From Ryan-Anderson et al, 2021.

Their paper introduced me to the delightful acronym: “state preparation and measurement (SPAM)” error. Plus, kudos to the scientists for providing pseudocode in the paper’s Appendix F.

In the Summary article to their result: “This is a significant advance,” says Laird Egan, a quantum engineer at the Maryland-based company IonQ, which had their own QEC research published, two months earlier.

Two Foundational QEC Results

Egan et al, 2021‘s work: Fault-tolerant control of an error-corrected qubit was one of two QEC successes, highlighted in Nature, in the November 19, 2021 Nature lead: “First quantum computer to pack 100 qubits enters crowded race”. In that group’s October 4 publication, they reported a fully error-corrected, quantum physical system with native noise characteristics made from 13 trapped ¹⁷¹Yb⁺ qubit ions, arranged appropriately for the QEC code.  Their report included error-rate numbers: a measurement error of 0.6% and a ‘Clifford gate error’ of 0.3%, which are related to the Pauli basis qubit errors. That error numbers are reported is notable. I expect to see reported errors more often, moving into applications from theory as QEC progresses.

A work from the Google Quantum AI group: Exponential suppression of bit or phase errors with cyclic error correction is the second QEC success highlighted in the November 19, 2021 Nature lead. Their work was also foundational in nature, demonstrating a QEC implementation using one-dimensional repetition codes embedded in a two-dimensional grid of qubits, with different quantum hardware:  21 superconducting qubits. The details at their blog, show how this system can allow one to better explore how logical errors decrease as logical qubit size grows.

Most remarkable for me, is the sensitivity of this technique found high-energy particles such as cosmic rays striking the quantum processor and decreasing the spin state lifetime on all qubits. Their reported error: median CZ operator Pauli error is 0.62% is similar to the previous Egan et al, 2021 result, 2021 and shows another valuable incremental progress on the long QEC road.

Reducing Transmon Error for NISQ Algorithms Today

Eric Holland, Director Strategic Growth Initiatives, was a good Twitter pointer to my final QEC note, setting the stage for the New Year 2022.

One of my predictions for 2022 is that we’ll see record low 2Q error rates in #quantum gates from tunable superconducting qubit architectures. One paper not to sleep on is this work from Eliot Kapit and @schusterqed

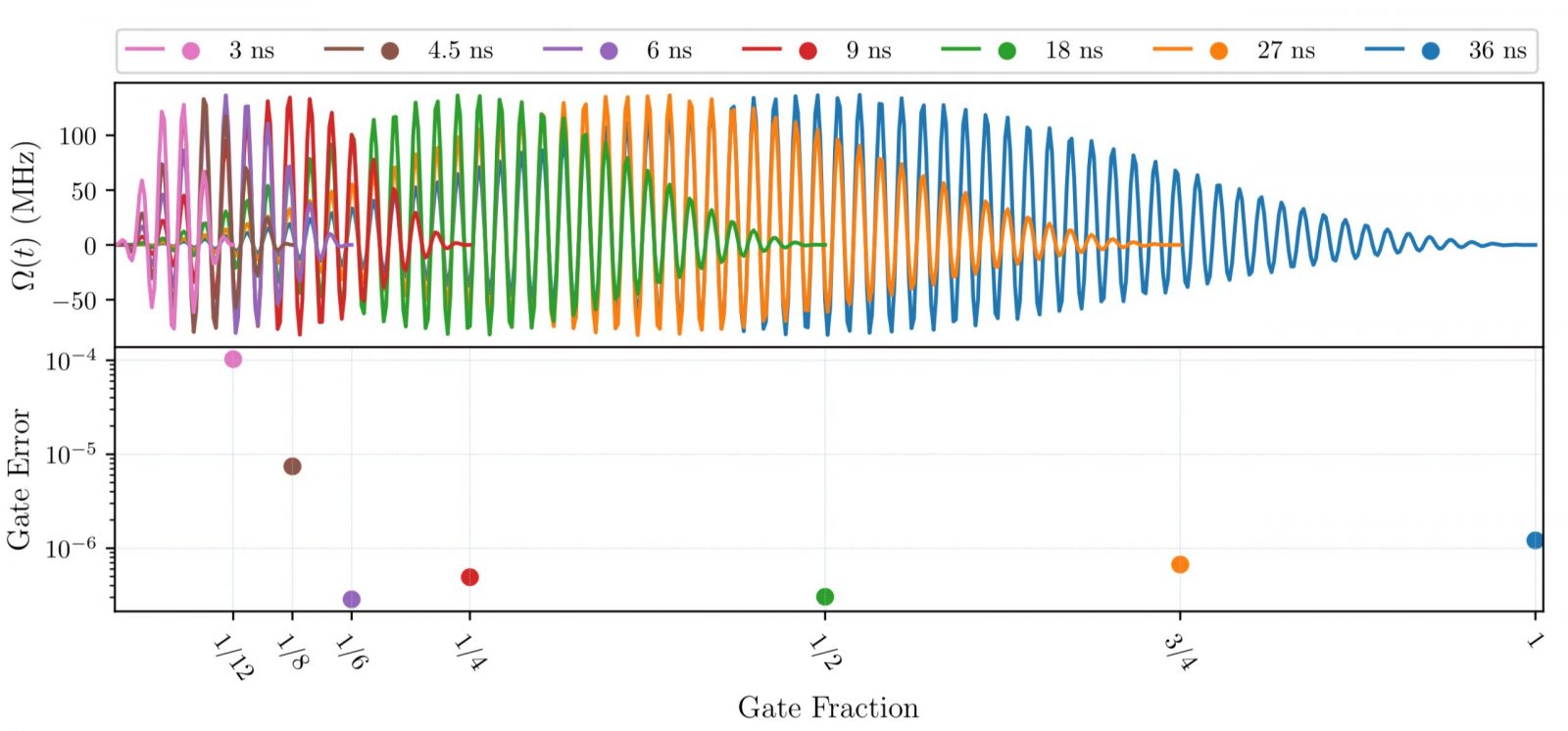
The reference by Holland is to Perez et al, 2021’s work, titled: Error-divisible two-qubit gates, which is a proposed method to significantly reduce two-qubit gate errors on transmon superconducting architectures, and any other system with tunable coupler circuit such as flux qubits and fluxoniums. Why address these two-qubit gate errors? The authors write that the inaccuracy of modern quantum algorithm implementations is dominated by two-qubit gate errors, as single-qubit gate errors are typically an order of magnitude smaller. The method succeeds by generating a fast-oscillating waveform that can cancel dispersive shift effects See Fig. 3. The authors write that, if their protocols were implemented at scale, then noisy intermediate-scale quantum (NISQ) algorithms would be significantly improved.

Figure 3. Fractional gates using the same set of parameters. {A, f, α, c} = {82.645 MHz, 1.868 GHz, 1.333, 0.336} (top) to get the gate errors {1.21, 0.67, 0.30, 0.49, 0.29, 7.43, 102.99} × 10−6(bottom). From Perez et al., 2021.

As we enter the New Year 2022, it’s worth to see how far QEC has come.

Interest to be acquainted with the QEC subject has grown, since Shor proposed his elegant quantum error correction scheme in 1995. Now the quantum-curious are active, as seen by Wikipedia’s Quantum Error Correction entry showing 263,388 total accesses (Dec 31, 2021) since its inception.

The Wikipedia page can even provide a metric of interest in quantum computing news events, such as the early October 2019 Physics World article which, without Wiki links from the press report, resulted in a spike of 5 times higher page accesses on October 3, 2019.

I find it fitting that the Wiki QEC entry page can now be a sensitive ‘detector’ to the international interest in the quantum computing environment. Happy 2022, QEC workers!